математика для детей

Автор Наталья Чистклетова

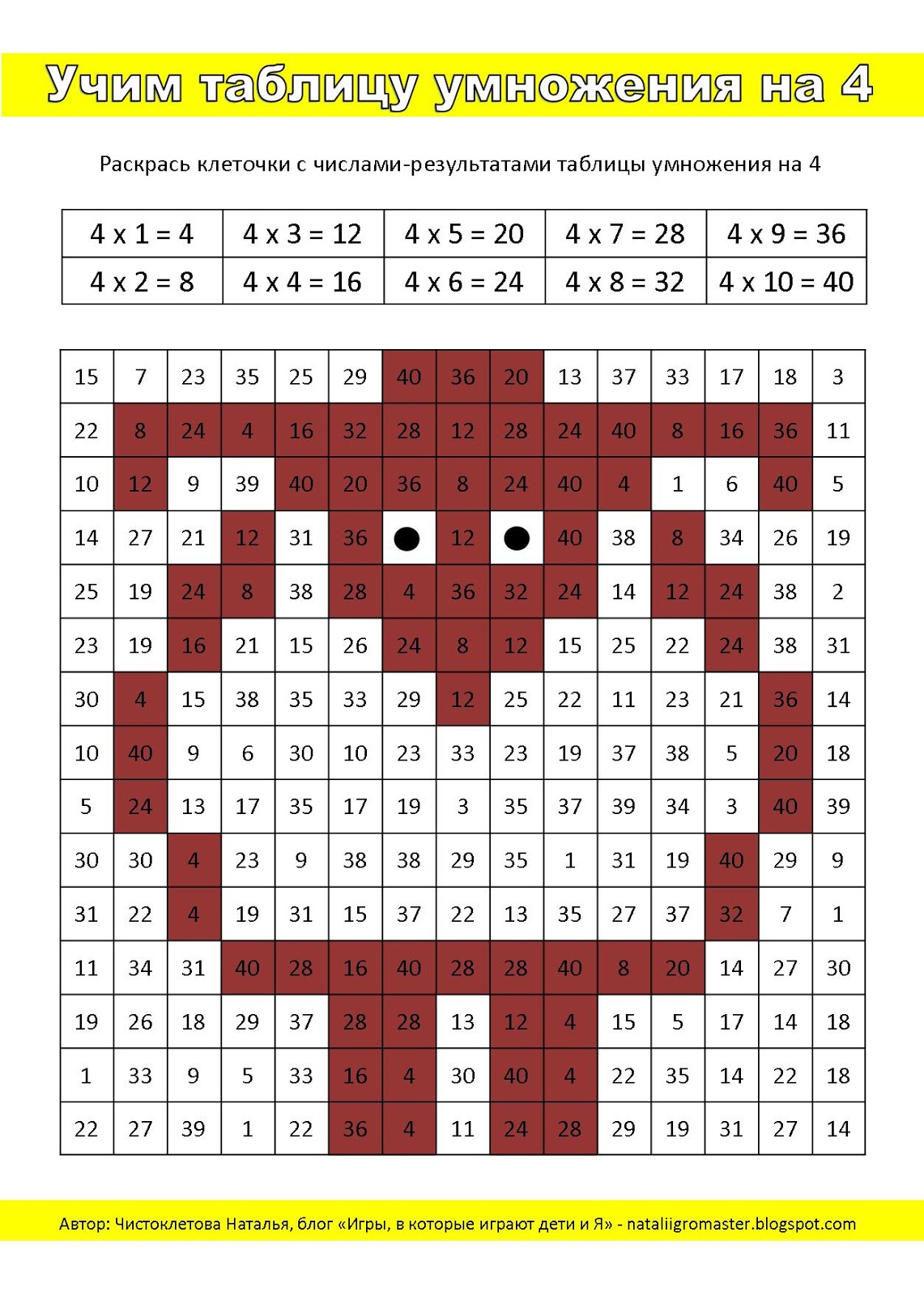
Делюсь с вами примерами-раскрасками, на изучение-закрепление таблицы умножения на 2, 3 и 4.

Первая страничка с ответом для родителя-учителя.

Отправлено спустя 2 минуты 53 секунды:

Отправлено спустя 1 минуту 46 секунд:

Об одном принципе Сингапурской математики

Недавно получила письмо от одной мамы, в котором она спрашивает, имеет ли учитель право ругать ее ребенка за то, что тот решает задачу своим способом. Не тем, который учитель рекомендовал. Речь не о чем-то спорном и заковыристом. Всего лишь счетная задачка. Для первоклассника.

На уроке учительница объясняла детям, как складывать числа. Вот, к примеру 7 и 8. Дополняем первое число до 10-ки. 7+8 = 7+3+5=10+5=15. И вот именно таким образом она просила учеников записывать решение.

А ребенок, о котором речь идет, делал не так. 7+8 = 5+5+2+3 = 10+5 = 15. Уж не знаю почему, — писала мне мама, но у него лучше получается 5-ками складывать. — Он мне объяснял, что их как будто видит. Как числа распадаются на 5-ки и небольшие остатки.

И вот вместо того, чтобы дополнять число до 10-ки, как требовал учитель, ребенок все слагаемые раскладывал на 5-ки. За что регулярно получал от учителя «на орехи».

Я в связи с этой историей вспомнила недавно купленный мною учебник по математике. Из Сингапурской программы. Там есть предисловие для учащихся. Для первоклассников. Даже не предисловие, а рекомендации – как работать с учебником и изучать математику.

Прочитай задачу и попытайся ее решить. Только после того, как решение найдено, загляни в раздел «Ответы».
Если твое решение совпадает с тем, что находится в разделе «Ответы», отлично! Если ты использовал другой метод, поздравляем! Теперь ты знаешь как минимум 2 способа решения задачи.
Если ответ не совпадает с тем, что в учебнике, просмотри свое решение еще раз. Попробуй понять, где ты допустил ошибку.
Когда ты поймешь, как решают задачи, разобранные в начале каждого раздела, переходи к практическим заданиям. Сверяй свои ответы с ответами в конце учебника. Если у тебя возникнут трудности с той или иной задачей, не паникуй. Попробуй прочитать задание еще раз и продумать каждый шаг к его решению. Если не получается, попроси помощь у друга или учителя.
Если ты прорешал все задания в разделе, то готов к более трудным упражнениям. Испытай себя! Делай их самостоятельно. Обращайся к учителю, только в случае острой необходимости.
Попробуй задать похожие вопросы своим друзьям и приятелям. Обсудите все возможные решения, их достоинства и недостатки.

Как вам? Оценили второй пункт? На мой взгляд, вот это стремление не дрессировать учеников, а помочь им понять, увидеть изучаемые концепции с самых разных сторон, и делает Сингапурскую программу по математике одной их самых сильных в мире. В сочетании с поразительной методичностью и глубиной изучения материала оно дает потрясающие результаты.

Знаете, с чего начинается учебник для 6-леток? С простенького задания посчитать мячики.

И вопроса – как ты думаешь, единственным ли образом можно это сделать? А как ты можешь быть уверен, что не пропустил ни один мячик? Попробуй придумать свой способ.

И далее приводится вариант авторов учебника. Можно вот так мячики считать.

А можно вот так.

Меня эта вариативность, эта степень свободы, более того, призыв к ней, очень радуют. И немного удивляют. Принято считать, что азиатские системы преподавания – это муштра, муштра и еще раз муштра. «Просто они вкалывают больше», — говорят люди. Согласна, вкалывают. Но дело, как выясняется не только в этом. Вкалывать можно по-обезьяньи, заучивая алгоритмы и на автомате выполняя то, что говорит учитель. А можно вкалывать, вдумываясь в суть изучаемого материала. Пробуя так, и этак, понимая, откуда что берется.

Чувствуете разницу?

PS: Кстати, я не утверждаю, что в Сингапурской программе совсем нет алгоритмов. Напротив. То же наглядное моделирование — дети учатся визуально представлять задачу с помощью прямоугольных блоков, которые помогают им увидеть соотношение между известными и неизвестными и найти решение. Но к этому методу они подходят постепенно. Пробуя самые разные способы представления данных. И, в конце концов, осознавая, зачем им, собственно, нужны именно прямоугольники.

Встретились мама- второклассницы и учитель девочки.
Мама-» Как дела в школе?»
Учитель-» Это хорошо, это неплохо.. А вот с задачками проблема..и решает как бы верно, но записывает не так как надо. »
Мама, немного задумавшись -» Я вот подумала и поняла, что в моей жизни ответы везде нужны, а вот применение записи нигде не пригодилось.»
Учитель-» Может вы и правы…..»
Вывод: главное при обучении: важны те знания, которые мы можем применить в жизни.

математика для детей ⇐ Воспитание детей